「アニメーションエクササイズ集」
グラフエディター練習
グラフエディター練習
「レベル」
レベル1「12原則を学ぶ段階」「3Dプログラムを学ぶ段階」
「概要」
「概要」
Translate(移動)編
簡単なオブジェクト(sphereや cube等)を使い
簡単なオブジェクト(sphereや cube等)を使い
ー直線
ー斜め
ー8の字
ー円
等の動きをつける。
そしてグラフがどうなるか理解する。
ー斜め
ー8の字
ー円
等の動きをつける。
そしてグラフがどうなるか理解する。
Rotate(回転)編
人間リグの腕等を使い上記と同じ事をRotation(回転)でやる。
「学べる内容・目的」
ーグラフエディターの使い方
ーどういうグラフと組み合わせがどういう動きをするのかの理解
------------------------------------------------------------------------------------------------
このエクササイズは2Dだとまったく必要ない奴なんですが。3Dでアニメーションをやる際、回転Rotationとか移動TranslateのXYZの数値とグラフエディタのグラフの関係をわかっていると3Dアニメーションをやるうえでとても役に立つのです。
ーどういうグラフと組み合わせがどういう動きをするのかの理解
------------------------------------------------------------------------------------------------
このエクササイズは2Dだとまったく必要ない奴なんですが。3Dでアニメーションをやる際、回転Rotationとか移動TranslateのXYZの数値とグラフエディタのグラフの関係をわかっていると3Dアニメーションをやるうえでとても役に立つのです。
まあ実際、数学とかいろいろあるのでしょうけど、
こういうグラフの形なら、こうなる!というのを理解するためにとても役立ちますし、一度自分でやってみると、感覚的にもつかめてよいです。
(赤い線に囲まれている部分が1サイクルになります。)

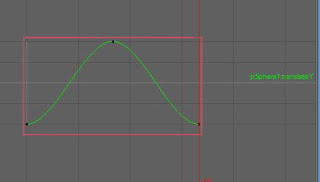
例えば、このボールのサイクル。これは上下(TlasnlateY軸)で動いているので、こういうグラフの形になります。
これはまあ、とても単純だし簡単ですよね。

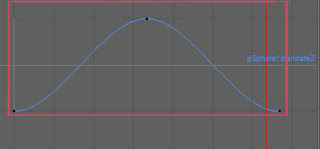
で、これは左右に動いてるやつ、これはTlanslateZ軸ですが、3D空間なので、手前と奥に動く場合はTlanslateX軸に同じグラフの形になりますね。
どちらの例も40フレームあります、で、グラフの形は(キャプチャーの仕方でちょっと違って見えますが、)全く同じです。
では上の二つのグラフを組み合わせたらどういう動きになるでしょう?

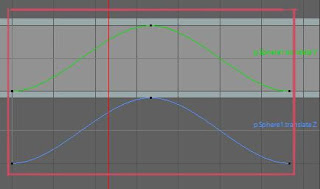
こういう感じで斜めの動きになります。
じゃあ、Tlanslate Zを反転させたら?

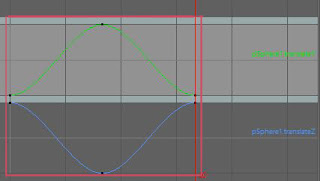
逆側の斜めの動きになります。
じゃあ、同じ感じで、ボールに円を描かせたかったらどういうグラフになるんでしょう?

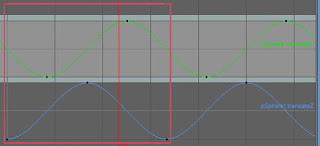
グラフの形はまったく同じです。ですが、ZとYのタイミングを半分ずらす。すると、きれいな円を描きます。
じゃあ、次は8の字です。どうなるでしょう?

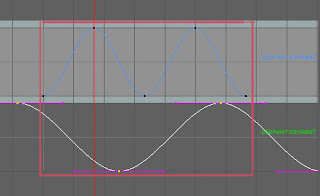
Zを二倍の速さにして、TZのタイミングを少しずらすと、このように八の字に。(またこれだとZを二倍にしていますが、Yを二倍の速さにすると∞みたいな横八の字になります。)
と、グラフのタイミング等をずらすだけで、こんなにいろいろとバリエーションができるのです。この各数値の組み合わせでどういう動きになるか?というのを少しでもわかっていると3Dアニメーションをやるうえでとても役に立ちます。。
この例ではMayaを使っているので、Yが上下軸になっていますが、どの軸がどの方向でも3Dプログラムは大体この3軸で場所を指定する、というものなので、どういう組み合わせがどういう動きを作る、というのさえ押さえておけば応用は聞くと思います。
で、このボールの例は移動軸ですが、回転軸でも似たことができます。
例えば人間リグだったら、FKの時の腕なんかで使えます。

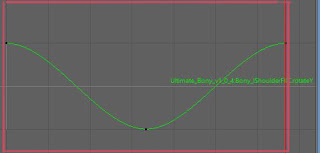
リグによっては軸の方向が違ったりするので、これはUltimateRigsというリグを使った場合ですね。
回転のYを、さっきのボールと同じ調子で動かすと、こう、左右に腕を振る動きができます。

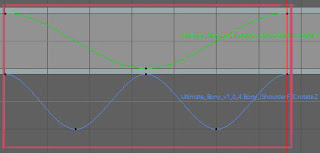
で、そこにYの二倍の速さのZの回転を加えると、こういう風に半円で腕ふりをするような動きになります。

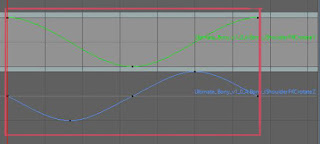
こちらは腕を一回転です。ボールと一緒で同じ形のグラフを半分ずらすとこの動きになりますね。

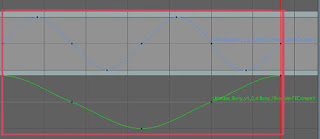
そして八の字、これは半円の動きのグラフ(Zが二倍)からZをちょっとずらすとこうなります。
ここに上げただけでなく、グラフを少しづつずらしたり、タイミングを変えたりして、腕やボールの動きがいったいどんな風になるか、グラフと照らし合わせつつ色々試してみましょう。
これをやるだけでかなりグラフに対しての動きの理解が深まります!
こういうグラフの形なら、こうなる!というのを理解するためにとても役立ちますし、一度自分でやってみると、感覚的にもつかめてよいです。
(赤い線に囲まれている部分が1サイクルになります。)


例えば、このボールのサイクル。これは上下(TlasnlateY軸)で動いているので、こういうグラフの形になります。
これはまあ、とても単純だし簡単ですよね。


で、これは左右に動いてるやつ、これはTlanslateZ軸ですが、3D空間なので、手前と奥に動く場合はTlanslateX軸に同じグラフの形になりますね。
どちらの例も40フレームあります、で、グラフの形は(キャプチャーの仕方でちょっと違って見えますが、)全く同じです。
では上の二つのグラフを組み合わせたらどういう動きになるでしょう?


こういう感じで斜めの動きになります。
じゃあ、Tlanslate Zを反転させたら?


逆側の斜めの動きになります。
じゃあ、同じ感じで、ボールに円を描かせたかったらどういうグラフになるんでしょう?


グラフの形はまったく同じです。ですが、ZとYのタイミングを半分ずらす。すると、きれいな円を描きます。
じゃあ、次は8の字です。どうなるでしょう?


Zを二倍の速さにして、TZのタイミングを少しずらすと、このように八の字に。(またこれだとZを二倍にしていますが、Yを二倍の速さにすると∞みたいな横八の字になります。)
と、グラフのタイミング等をずらすだけで、こんなにいろいろとバリエーションができるのです。この各数値の組み合わせでどういう動きになるか?というのを少しでもわかっていると3Dアニメーションをやるうえでとても役に立ちます。。
この例ではMayaを使っているので、Yが上下軸になっていますが、どの軸がどの方向でも3Dプログラムは大体この3軸で場所を指定する、というものなので、どういう組み合わせがどういう動きを作る、というのさえ押さえておけば応用は聞くと思います。
で、このボールの例は移動軸ですが、回転軸でも似たことができます。
例えば人間リグだったら、FKの時の腕なんかで使えます。


リグによっては軸の方向が違ったりするので、これはUltimateRigsというリグを使った場合ですね。
回転のYを、さっきのボールと同じ調子で動かすと、こう、左右に腕を振る動きができます。


で、そこにYの二倍の速さのZの回転を加えると、こういう風に半円で腕ふりをするような動きになります。


こちらは腕を一回転です。ボールと一緒で同じ形のグラフを半分ずらすとこの動きになりますね。


そして八の字、これは半円の動きのグラフ(Zが二倍)からZをちょっとずらすとこうなります。
ここに上げただけでなく、グラフを少しづつずらしたり、タイミングを変えたりして、腕やボールの動きがいったいどんな風になるか、グラフと照らし合わせつつ色々試してみましょう。
これをやるだけでかなりグラフに対しての動きの理解が深まります!